In ogni caso, hanno torto:

Sette ASCII casuali stampabili: 95 ⁷ = 69 833 729 609 375 possibili password.

Dieci alfabetici casuali: 52 ¹⁰ = 144 555 105 949 057 024 possibili password o oltre 2000 volte di più.

La lunghezza conta. Se generi le tue password in modo casuale, conta molto più di qualsiasi altro metodo per renderle difficili da indovinare.

La prospettiva teorica

Facciamo i conti qui. Ci sono 26 lettere, 10 cifre e diciamo di 10 caratteri speciali. Per cominciare, assumiamo che la password sia completamente casuale (e che un personaggio di un gruppo non sia più usato da un personaggio di un altro gruppo).

Il numero di password possibili può quindi essere scritto come C = s^n dove s è la dimensione dell'alfabeto e n il numero di caratteri. L'entropia della password è definita come:

log2(C) = log2(s^n) = log2(s)*n

Consente di collegare i numeri della domanda in questo:

     s    n   Entropy (bits)
A   52    6   34.2
B   52   10   57.0
C   72    7   43.2
D   26   10   47.0
E   26    5   23.5

Quindi in questo scenario, C è solo la terza opzione migliore, dopo B e D.

La prospettiva pratica

Ma tutto questo è sotto l'ipotesi della casualità. Questo non è un presupposto ragionevole per come le persone generano password. Gli umani semplicemente non lo fanno in questo modo. Quindi dovremmo scegliere alcune altre ipotesi su come vengono generate le password, e quale ordine l'aggressore li prova nel suo dizionario.

Un'ipotesi non irragionevole sarebbe che molti dizionari iniziano con le parole, e solo in seguito passerai a fare sostituzioni e aggiungere caratteri speciali. In tal caso, un singolo carattere speciale in una password corta sarà meglio di una parola comune molto lunga. Ma d'altra parte se l'attaccante sa che viene sempre usato un personaggio speciale, prima tenterà di provare quelle password. E sulla terza mano forse il dizionario è incentrato su principi completamente diversi (come l'occorrenza nei database trapelati).

Potrei continuare a speculare per sempre.

Perché è la domanda, non le risposte, è sbagliato

Il problema è che ci sono molti principi su come viene generata la password tra cui scegliere, e potrei sceglierne uno arbitrariamente per fare quasi tutte le risposte corrette. Quindi l'intera domanda è inutile e serve solo a oscurare un punto importante che nessuna politica sulle password nel mondo può applicare: Non è ciò che contiene una password che lo rende strong - è come viene generato.

Ad esempio, Password1! contiene maiuscolo, minuscolo, un numero e un carattere speciale. Ma non è molto casuale. ewdvjjbok invece contiene solo lettere minuscole ma è molto meglio dato che è generato casualmente .

Cosa avrebbero dovuto fare

Se semplicemente smetti di affidarti alla memoria umana molto fallibile e limitata, il set di caratteri e la lunghezza smettono di essere fattori limitanti che devi pesare l'uno contro l'altro. Puoi avere entrambi in abbondanza.

Un modo per farlo è usare un gestore di password. Come indicato da Dan Lowe nei commenti, questa potrebbe non essere un'opzione praticabile in un ospedale. Una seconda alternativa consiste nell'utilizzare una sorta di autenticazione a due fattori (ad esempio un token o una keycard hardware) che rende meno importante la sicurezza del primo fattore (la password).

Questa è la responsabilità dei responsabili di sistema e non degli utenti finali da implementare. Devono fornire gli strumenti che consentono agli utenti finali di svolgere il proprio lavoro in modo pratico e sicuro. Nessuna quantità di educazione dell'utente può cambiarlo.

Mi rendo conto che ci sono già una serie di buone risposte, ma voglio chiarire un punto.

La domanda è irrisolvibile in quanto non specifica un set di caratteri, né il metodo di selezione della password.

Prima di affrontare il secondo punto, faremo finta che le password siano generate in modo veramente casuale all'interno del dominio consentito, altrimenti non potremo nemmeno iniziare a ragionare sull'argomento.

Per il nostro altro punto, per dare esempi estremi, diciamo che b implica lettere solo nell'alfabeto inglese, quindi diciamo 52 possibili simboli. Ciò fornisce circa 5,7 bit di entropia per carattere e quindi circa 57 bit di entropia complessiva.

D'altro canto, diciamo (forse in qualche modo irragionevolmente) che la risposta c implica un punto di codice Unicode completamente casuale che è considerato un carattere (al contrario di una BOM, ecc.). Attualmente ne esistono all'incirca 109.000 a partire da Unicode 6. Ciò significa circa 16,7 bit di entropia per carattere e un totale di 117 bit di entropia.

D'altra parte se la risposta c era limitata a solo ASCII o forse a ISO 8859-15 oa qualche sottoinsieme di questi, la conclusione opposta potrebbe essere facilmente tracciata.

Questo è ovviamente del tutto irragionevole, ma evidenzia la scomposizione della domanda e come si possa ragionevolmente giustificare una delle due risposte. Per essere una domanda di test sensata dovrebbe essere formulata in modo molto più rigoroso, il che renderebbe molto più difficile per gli utenti con conoscenze tecniche o matematiche limitate di elaborare.

Alla fine suggerirei che questo test sia probabilmente abbastanza inutile in quanto un'organizzazione non richiederebbe agli utenti di memorizzare i requisiti delle password, ma li imporrebbe tecnologicamente (l'unico requisito che posso pensare che l'apprendimento a memoria sia utile non è il riutilizzo la stessa password in più posti).

L'NHS ha torto su quali password sono più sicure nel caso ideale? Sì, assolutamente - e le altre risposte hanno coperto abbastanza bene questo campo.

L'NHS ha torto su quali password sono più sicure in un ambiente NHS? Forse no.

Come potrebbe una password lunga essere peggio tha -?

Esistono sistemi legacy che limitano artificialmente la lunghezza di una password, ad esempio il vecchio hash della password Windows LANMAN / NTLMv1 limita la lunghezza a 14 simboli e il vecchio hash della password UNIX basato su DES lo limita a 8. Peggio ancora , l'immissione della password su un sistema di questo tipo ti consente spesso di inserire una password per tutto il tempo che desideri e di ignorare tutto dopo i primi simboli n .

In effetti, sembra probabile che NTLMv1 sia il particolare schema legacy che stanno utilizzando. Come sottolinea @MarchHo, NTLMv1 divide la tua password in due metà di un massimo di 7 caratteri ciascuna e ciascuna metà può essere decifrata separatamente. Quindi, se stai usando NTLM con una password alfanumerica di 10 caratteri, quello che hai veramente è una password alfanumerica di 7 caratteri e una password alfanumerica di 3 caratteri. Il primo è chiaramente peggio di 7 caratteri del set completo di simboli e quest'ultimo può essere interrotto in millisecondi su un PC di 10 anni.

Perché una cosa così vecchia sarà ancora in uso?

Fondamentalmente, perché funziona e sarebbe costoso aggiornare.

Ora, questa sono le mie ipotesi, ma: propongo che gli ambienti sanitari, in particolare, utilizzeranno probabilmente sistemi legacy, a causa della natura sensibile dell'assistenza sanitaria. È probabile che i nuovi sistemi necessitino di un controllo approfondito prima di essere accettati come soluzione, il che significa che gli aggiornamenti dei sistemi sanitari tendono ad accadere lentamente e con grandi spese.

Quindi, se sai che ci sono dei sistemi di uso comune che si comportano in questo modo, e non puoi correggerli, allora il meglio che puoi fare è dire ai tuoi utenti di scegliere una lunghezza- n password utilizzando il più grande pool di simboli possibile.

In generale: sei sicuro che le tue password non siano troncate?

Sfortunatamente, questo ha implicazioni anche per il caso generale, specialmente per noi che amiamo le nostre password a lungo. Quanto siamo sicuri di non poter accedere al nostro account sul link solo con la prima o due parole chiave della nostra passphrase? Tanto male che usare la ben nota "correttezzabatteriapiedi" è, accidentalmente, usare "corretto" sarebbe anche peggio. Per essere sicuro nelle tue password non è sufficiente per essere sicuro di generare abbastanza entropia. Devi anche essere sicuro che il sistema dall'altra parte non stia buttando via la maggior parte di esso.

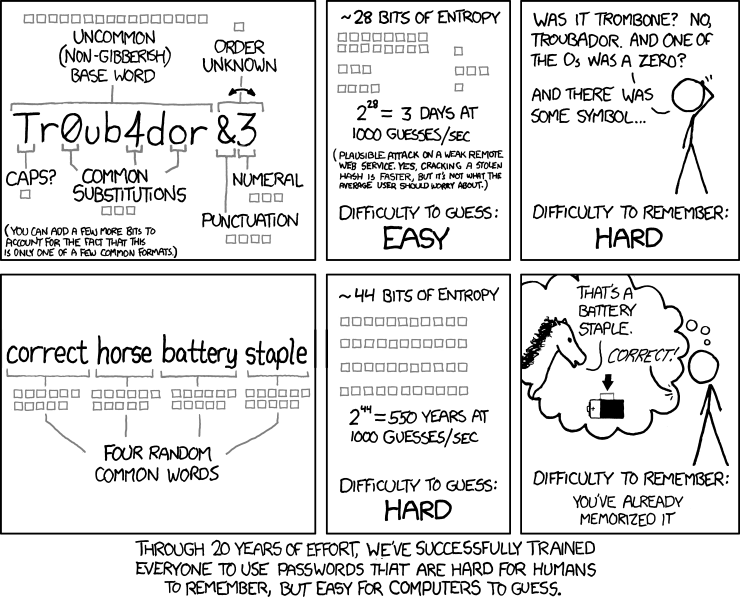
Ci sono alcuni problemi con quella domanda. Uno di questi è che non indica come vengono scelte le password, ma ritengo che l'approccio più logico sia quello di presumere che le password siano scelte casualmente ma soddisfino le condizioni rispettive, quindi userò tale convenzione per la mia risposta. Si noti che il fumetto di Randall chiaramente non condivide questa ipotesi, ma la domanda non ha specificato in che modo viene scelta una password, quindi penso che possiamo andare per il meglio che è possibile e che è scegliere una password a caso. Inoltre, il test probabilmente non si basa sul fumetto di Randall.

Il ritmo chiave dell'opzione b è abbastanza semplice da calcolare se assumiamo che l'alfabeto inglese sia usato. Sì, più ipotesi, lo so. Ma dal momento che il test sembra essere in inglese e non molto difficile, penso che possiamo fare quella premessa.

Ci sono 26 lettere minuscole nell'alfabeto inglese e altrettante lettere maiuscole, per un totale di 52 caratteri. Quindi ci sono 52 ^ 10 ≈ 1.45 * 10 ^ 17 elementi nello spazio chiave dell'opzione b .

L'opzione c è molto meno specifica dell'opzione b . Tuttavia, poiché abbiamo assunto che venga usato l'alfabeto inglese - che è a favore dell'opzione c - possiamo anche supporre che solo l'ASCII sia usato per i caratteri speciali - che è a favore dell'opzione b . In realtà, se avessimo assunto più caratteri speciali di quelli di ascii, abbiamo dovuto assumere più lettere di quante ne siano in ascii poiché ä è in realtà una lettera in tedesco. Ciò rende lo spazio chiave dell'opzione b ancora più grande rispetto a quello dell'opzione c . *

Il meglio che possiamo fare per l'opzione c se ci limitiamo all'alfabeto ASCII è quello di utilizzare ogni carattere stampabile (escluso lo spazio vuoto) nel nostro alfabeto (nota: uso diverso e più generale della parola "alfabeto") . Sono 94 caratteri, l'opzione c è uno spazio chiave di 94 ^ 7 ≈ 6.48 * 10 ^ 13 elementi.

Dato che una delle nostre ipotesi per affrontare la domanda è che la password viene scelta casualmente tra le rispettive restrizioni e quella regola è uguale alla scelta casuale di una password dal rispettivo spazio chiave, una password scelta usando l'opzione b è discutibilmente più difficile da indovinare poiché ci sono diversi ordini di grandezza di più opzioni da provare quando si spezza la password.

Infatti, se ipotizziamo che i costi di cracking di una password tramite forza bruta siano approssimativamente lineari rispetto alla dimensione dello spazio tasti, cracking una password scelta tramite l'opzione b è 52 ^ 10 / (94 ^ 7) ≈ 2'229 volte più difficile del cracking scelto tramite l'opzione c , mostrando chiaramente che la presunta risposta corretta a questa domanda è sbagliata.

* Questo è abbastanza facile da provare matematicamente ma questo StackExchange manca di supporto per LaTeX e probabilmente lo capirai meglio attraverso una descrizione testuale comunque.

L'unica opzione di vantaggio c come sopra l'opzione b è il suo alfabeto più grande (ancora, uso più generale della parola "alfabeto"). L'opzione b , tuttavia, rende più che sufficiente optando per una password più lunga. Se aggiungiamo un numero sempre maggiore di caratteri (come ü , à , Ø , Æ , ecc.), Stiamo rendendo gli alfabeti più di dimensioni uguali, con il vantaggio di c su b a diminuire, mentre il vantaggio di b su c non viene modificato.

Adoro le domande di entropia:

La risposta breve:

Sì, sei "tecnicamente" corretto sull'avere più entropia (miglior tipo di corretto).

La lunga risposta

L'entropia è calcolata in gran parte da due fattori. Numero di simboli utilizzabili da una password e lunghezza. Nello scenario del NHS, sarebbe logico che "caratteri speciali" fossero simboli disponibili da utilizzare nella risposta 10 caratteri e quindi, più lunga è la password, maggiore è l'entropia e, teoricamente, più sicura.

TUTTAVIA, dobbiamo avere a che fare con le persone e siamo pigri. La domanda è cercare di convincere le persone a includere caratteri speciali nella loro password perché costringe l'entropia ad accadere.

Senza di esso, il fumetto di Randall è matematicamente corretto, pur essendo sfacciato, ma qualsiasi SysAdmin che crede che correcthorsebatterystapler sia una buona password perché deve essere schiaffeggiato in faccia, perché è stato nelle mie tabelle arcobaleno per un po '.

Per essere onesti, penso che prendere quattro parole del dizionario e metterle insieme sia un buon concetto (che è quello che chiamiamo una passphrase), tuttavia le persone come ho detto sono pigre e probabilmente cadranno per modelli comuni.

Sia il test quotato che i tuoi controargomenti sono errati, fondamentalmente perché l'entropia è una misura di casualità di una password, non la lunghezza, non la dimensione dell'alfabeto. Lo schema di fumetti XCKD che citi è sicuro per il livello di sicurezza a 44 bit rivendicato se e solo se le 44 piccole caselle grigie sotto "graffetta batteria cavallo corretta" rappresentano i risultati di lanci di monete (o uniforme simile, eventi casuali indipendenti) che sono stati usati per selezionare le password. Se un essere umano ha scelto le parole, tutte le scommesse sono state annullate.

Dato che né il NHS né parli di questo fattore critico, è impossibile dire qualcosa di concreto sulla sicurezza delle password, a parte il fatto che se non vengono scelti in modo uniforme a caso potrebbero essere deboli.

It is my understanding that as a rule, extending password length adds more entropy than expanding the alphabet.

Se d è la dimensione dell'alfabeto e n è la lunghezza della password, quindi una password scelta in modo uniforme a caso ha log2(d) * n bit di entropia. Raddoppiando la dimensione dell'alfabeto si aggiungono quindi n bit di entropia; aggiungendo un simbolo in più alla password, aggiunge log2(d) bit. Quindi tutto si riduce ai valori concreti di d e n ; non c'è davvero molto poco nell'avere una regola empirica come la stai proponendo lì, dal momento che possiamo semplicemente calcolare gli aumenti in modo diretto.

Ecco la cosa, che ti piaccia o no questa domanda non riguarda le password di laboratorio o matematicamente più sicure. Si tratta di convincere le persone a "pensare" alle loro password quando le scelgono.

a. È errato perché ha solo lettere.
b. è sbagliato perché ha solo lettere
c. è corretto perché è abbastanza lungo e include "caratteri speciali"
d. è sbagliato perché ha solo lettere.

In altre parole, le password che utilizzano solo lettere sono sbagliate.

Ora, è vero che puoi creare una password più sicura usando solo le lettere se è abbastanza lunga, o abbastanza casuale. Surly "asefhesesnh" è meglio di "p4ssw0rd!", Ma per essere onesti è una comprensione che va oltre la maggior parte delle persone nel pubblico di destinazione di questo test.

Invece è "meglio" far capire agli utenti di scegliere una password che sia "più lunga" e che abbia lettere, numeri e caratteri speciali.

In altre parole C è corretto quando parli di una vasta gamma di utenti con diversi livelli di abilità tecnica, creando le loro password. Sicuro che la matematica potrebbe essere spenta, ma non importa. Nessun fornitore, si siederà lì e scoprirà l'entropia della password, ma può contare il numero di $ in una password.

L'opzione b ti offre 52 possibilità per carattere.

Affinché c sia migliore, ognuno dei 7 caratteri deve avere più di 52 ^10/7 = almeno 283 possibilità.

Questo significa che i set di caratteri ASCII o western ANSI non sono sufficienti. Dovrebbero consentire il set di caratteri Unicode (o alcune codepage ANSI asiatiche molto arcane) in modo che l'opzione c sia migliore.

È ovviamente una domanda mal formulata. Ci sono 62 numeri e lettere (maiuscole e minuscole), quindi la risposta corretta sarebbe:

c se "caratteri speciali" significa che posso usare caratteri Unicode o qualsiasi altro set di caratteri che contenga almeno 221 caratteri non alfanumerici (cioè "speciali"), altrimenti b.